Algorithm For Chess Programming

Algorithm Types and Classification Gonit Sora. The speed of an algorithm is measured in terms of number of basic operations it performs. Consider an algorithm that takes N as input and performs various operations. The corelation between number of operations performed and time taken to complete is as follows consider N as 1,0. Ghz Problem whose running time doesnot depend on input size constant time. N operations 1. N operations 1 us. Nlog N opeartions 2. N operations Unimaginable time. Hence, it should be noted that every algorithm falls under certain class. Bip Files 3Ds Max'>Bip Files 3Ds Max. From increasing order of growth they are classified as constant time algorithm, logarithmic algorithm, linear time algorithm, polynomial time algorithm and exponential time algorithm. Formally, we denote the complexity of algorithm using asymptotic notation n read Theta of nThere are basically 3 asymptotic notation used. O Big O, omega. Mathematically, these are defined as follows For a given function gn,  we denote by gn the set of functionsgn fn there exist positive constants c. For a given function gn, we denote by Ogn  the set of functions. Ogn fn there exist positive constants c and n. For a given function gn, we denote by gn the set of functionsgn fn there exist positive constants c and n. Informally, Ogn establishes an upper bound on the function. Algorithm For Chess Programming' title='Algorithm For Chess Programming' />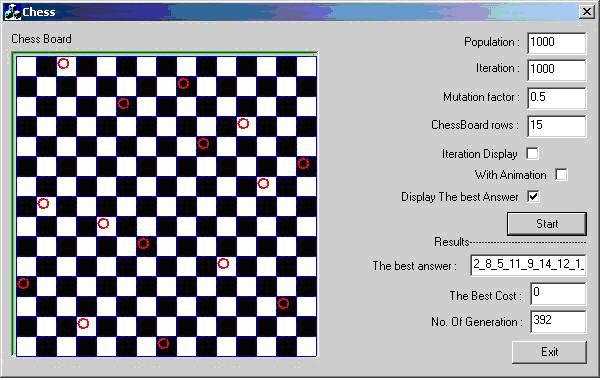Welcome to the Department of Computer Science at the University of Alabama at Birmingham. This  is used to denote the worst case runtime of an algorithm. This is used to denote the average runtime of an algorithm. We can use it to indicate the Best case runtime of an algorithm. We will use these notations to indicate the time complexity of algorithms that will be discussed later. Different types of algorithms Every algorithm falls under a certain class. Basically they are 1      Brute force. Divide and conquer. Decrease and conquer. Dynamic programming. Greedy algorithm. Transform and conquer. Backtracking algorithm. Brute force algorithm Brute force implies using the definition to solve the problem in a straightforward manner. Brute force algorithms are usually the easiest to implement, but the disadvantage of solving a problem by brute force is that it is usually very slow and can be applied only to problems where input size is small. Divide and conquer algorithm In divide and conquer method, we divide the size of a problem by a constant factor in each iteration. This means we have to process lesser and lesser part of the original problem in each iteration. Sexual_cycle.svg.png/531688352/420px-Sexual_cycle.svg.png' alt='Algorithm For Chess Programming' title='Algorithm For Chess Programming' />IMAGES wikieducator. First Computer Program algorithm to compute Bernoulli numbers 1841 1842 Ada Lovelace worlds first computer programmer began. Artificial intelligence AI The ability of a computer to perform tasks commonly associated with intelligent beings. The Food and Drug Administration announced today that 465,000 pacemakers installed in the US have a security vulnerability that could be exploited to make the device. RoboAvatars Chess Robot consists of a gantrymounted arm that picks up chess pieces and places them in their new location, as directed by the software. Some of the fastest algorithms belong to this class. Divide and conquer algorithms have logarithmic runtime. Candles Hey Monday. Decrease and conquer algorithm This kind of problem is same as divide and conquer, except, here we are decreasing the problem in each iteration by a constant size instead of constant factor. Dynamic programming The word dynamic   refers to the method in which the algorithm computes the result. Sometimes, a solution to the given instance of problem depends on the solution to smaller instance of sub problems. It exhibits the property of overlapping sub problems. Hence, to solve a problem we may have to recompute same values again and again for smaller sub problems. Hence, computing cycles are wasted. To remedy this, we can use dynamic programming technique. Introduction Delphi is one of the best programming tools to create software for Windows. With Delphi you can without much effort create small yet powerful Windows. Understandable C and C tutorials. Includes compiler setup, basic concepts up to pointers, arrays, classes, recursion, linked lists, and more. Methods of representation Methods of selection Methods of change Other problemsolving techniques Concisely stated, a genetic algorithm or GA for short is a. Algorithm For Chess Programming' title='Algorithm For Chess Programming' />Basically, in dynamic programming, we remember the result of each sub problem. Whenever we need it, we will use that value instead of recomputing it again and again. Here, we are trading space for time. A good example for a problem that has overlapping sub problem is the relation for Nth Fibonacci number. It is defined as Fn Fn 1 F n 2. Note that the Nth Fibonacci number depends on previous two Fibonacci number. If we compute Fn in conventional way, we have to calculate in following manner. The similar colored values are those that will be calculated again and again. Note that Fn 2 is  computed 2 times, Fn 3 3 times and so on. Hence, we are wasting a lot of time. Infact, this recursion will perform operations for a given N, and it is not at all solvable for N 4. PC within atleast a year. The solution to this is to store each value as we compute it and retrieve it directly instead of re calculating it. This transforms the exponential time algorithm into a linear time algorithm. Hence, dynamic programming is a very important technique to speed up the problems that have overlapping sub problems. Greedy algorithm For many problems, making greedy choices leads to an optimal solution. These algorithms are applicable to optimization problems. In a greedy algorithm, in each step, we will make a locally optimum solution such that it will lead to a globally optimal solution. Once a choice is made, we cannot retract it in later stages. Proving the correctness of a greedy algorithm is very important, since not all greedy algorithms lead to globally optimum solution. For ex consider the problem where you are given coins of certain denomination and asked to construct certain amount of money in inimum number of coins. Let the coins be of 1, 5, 1. If we want change for 3. According to this process, we select the coins as follows 2. For coins of given denomination, the greedy algorithm always works. But in general this is not true. Consider the denomination as 1, 3, 4 cents. To make 6 cents, according to greedy algorithm the selected coins are 4 1 1. But, the minimum coins needed are only 2 3 3Hence, greedy algorithm is not the correct approach to solve the change making problem. Infact, we can use dynamic programming to arrive at optimal solution to this problem. Transform and conquer Sometimes it is very hard or not so apparent as to how to arrive at a solution for a particular problem. In this case, it is easier to transform the problem into something that we recognize, and then try to solve that problem to arrive at the solution. Consider the problem of finding LCM of a number. Brute force approach of trying every number and seeing if it is the LCM is not the best approach. Instead, we can find the GCD of the problem using a very fast algorithm known as Euclids algorithm and then use that result to find the LCM as LCM a, b a b GCD a, b Backtracking algorithm Backtracking approach is very similar to brute force approach. But the difference between backtracking and brute force is that, in brute force approach, we are generating every possible combination of solution and testing if it is a valid solution. Whereas, in backtracking, each time you generate a solution, you are testing if it satisfies all condition, and only then we continue generating subsequent solutions, else we will backtrack and go on a different path of finding solution. Creare Un Keygen Torrent. A famous example to this problem is the N Queens problem. According to the problem, we are given a N X N sized chessboard. We have to place N queens on the chessboard such that no queens are under attack from any other queen. We proceed by placing a queen in every column and appropriate row. Every time we place a queen, we check whether it is under attack. If so, then we will choose a different cell under that column. You can visualize the process like a tree. Each node in the tree is a chessboard of different configuration.